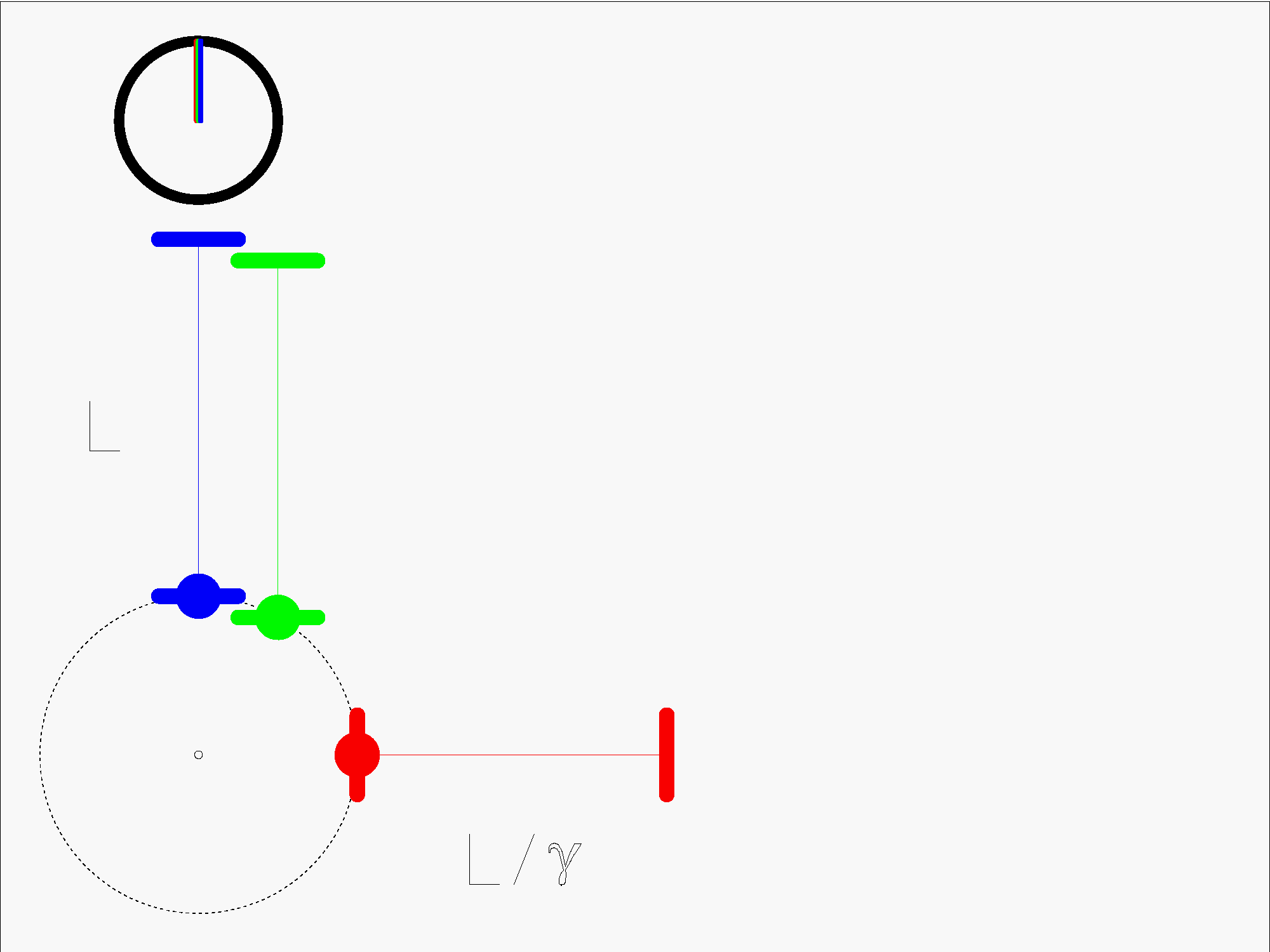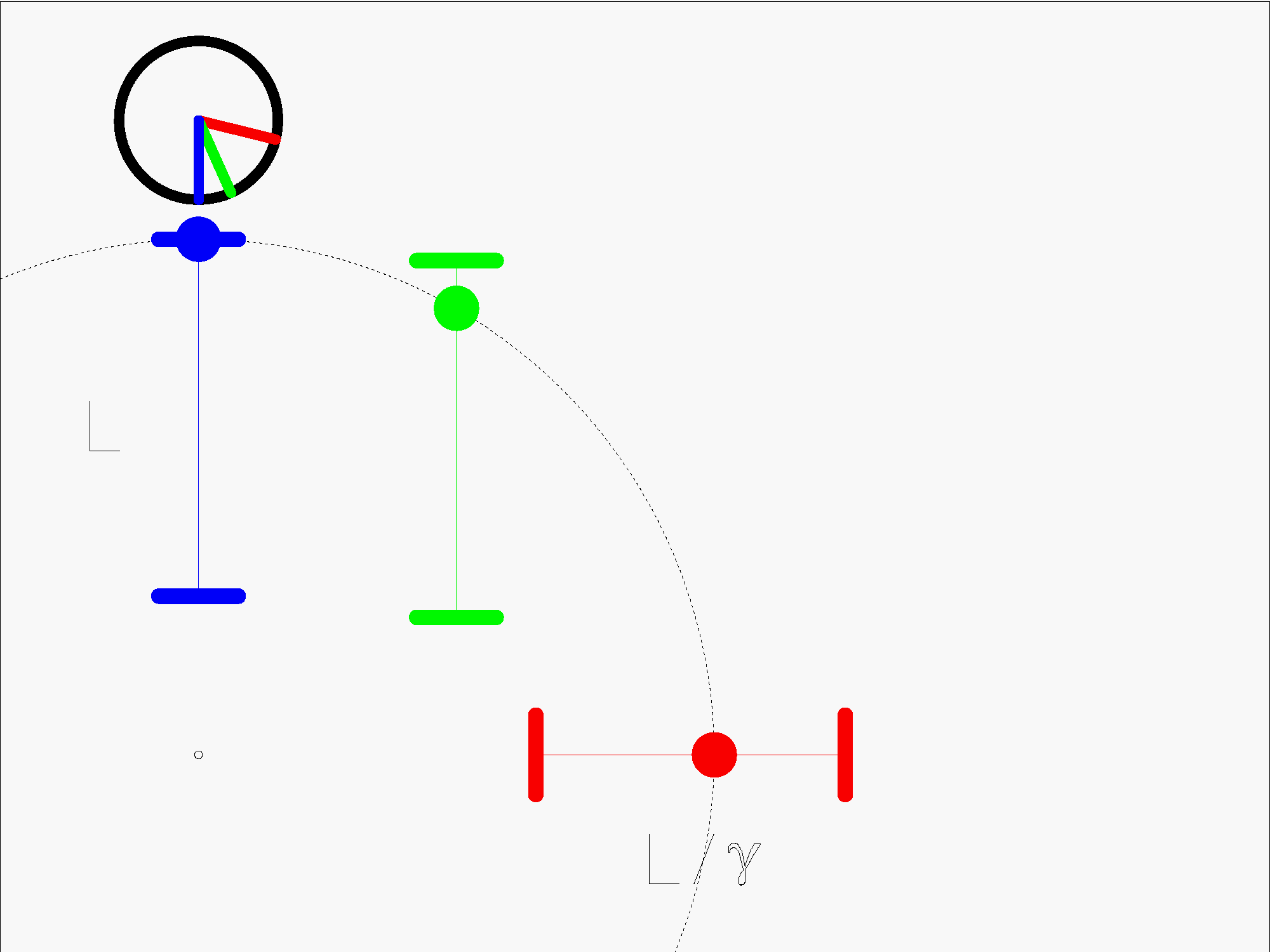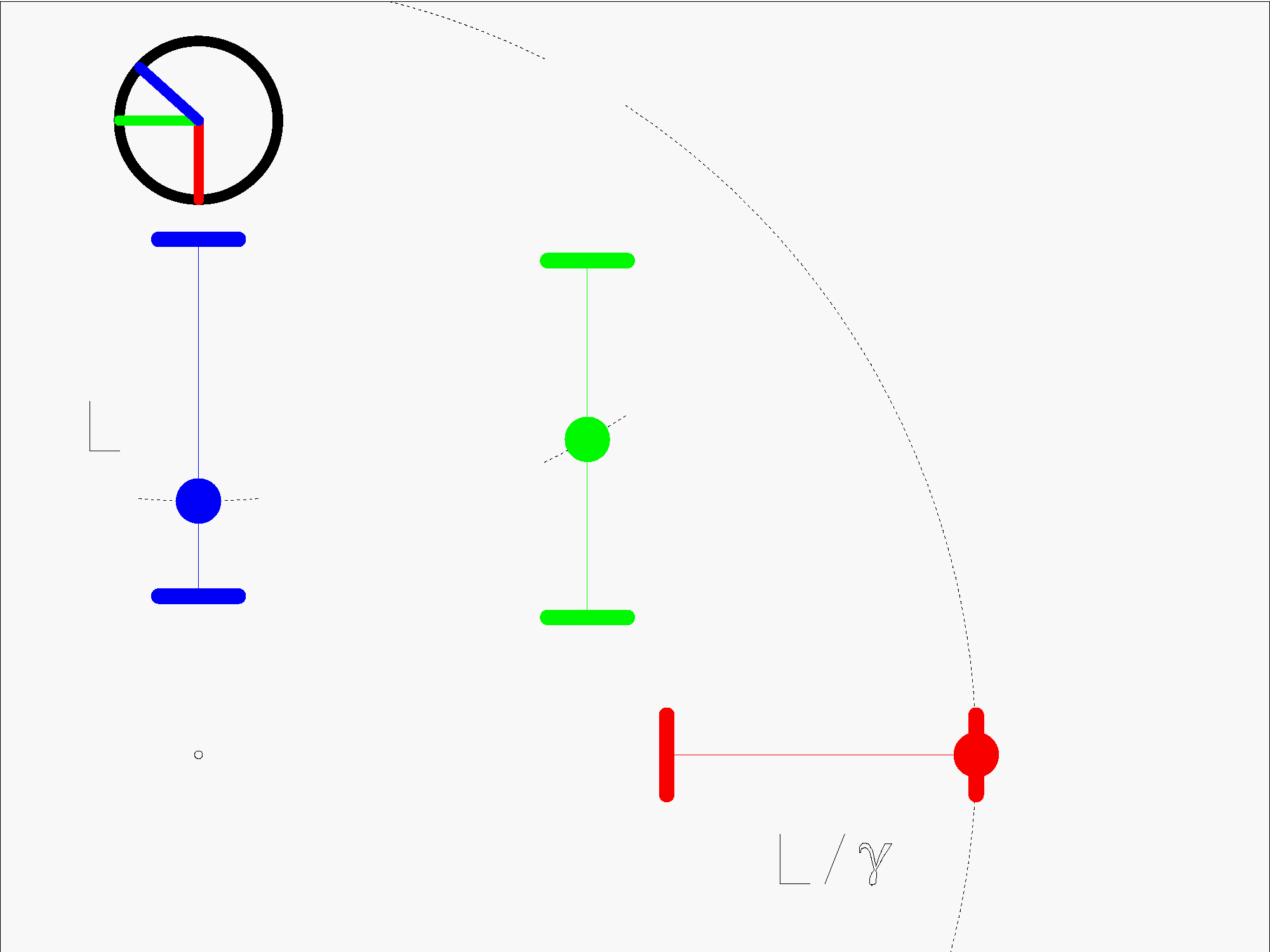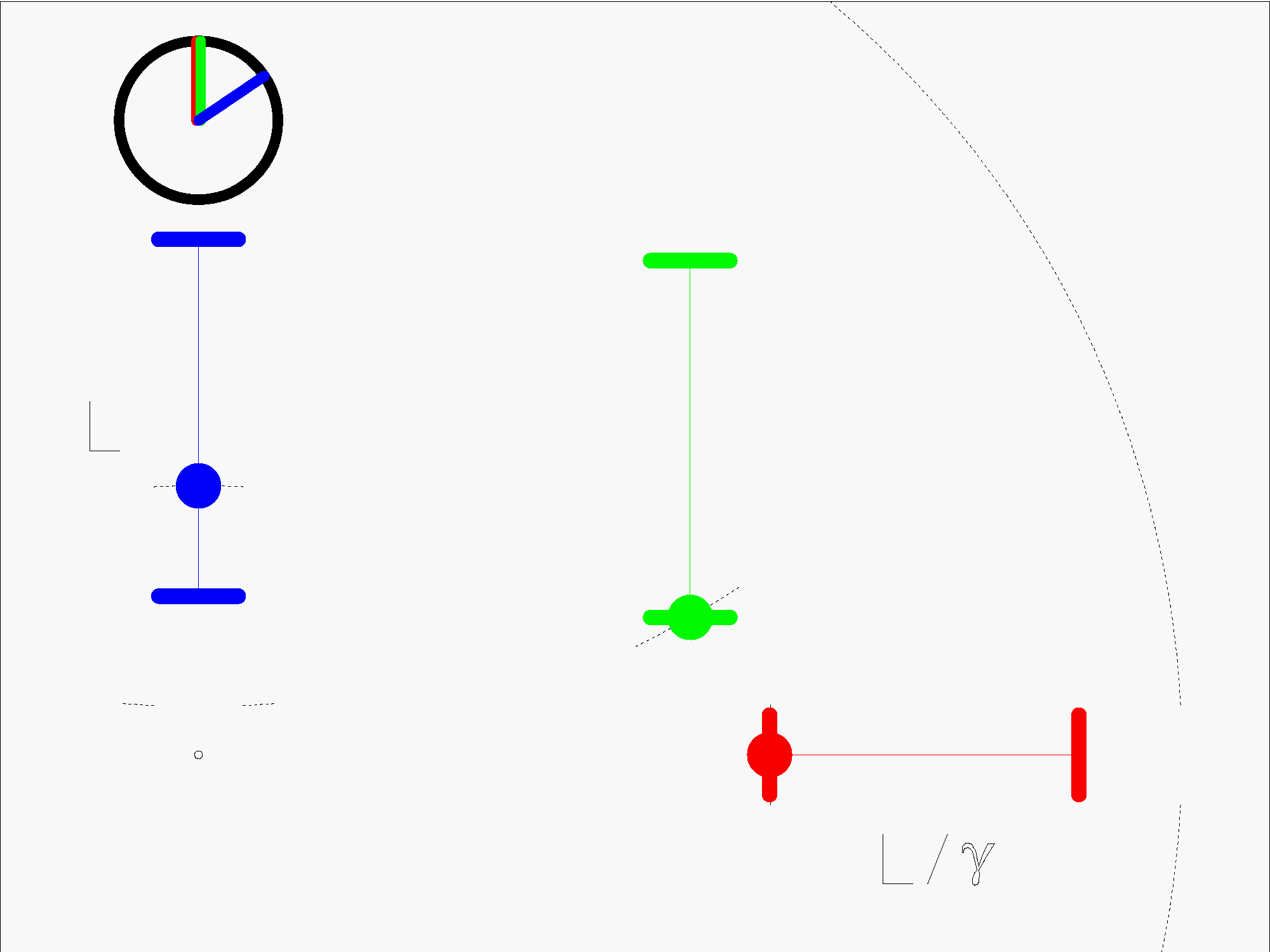
Bei der Lichtuhr läuft ein Lichtpuls zwischen zwei Spiegeln hin und her. Die Anzahl der Durchläufe ist ein Maß für die verstrichene Zeit. Normalerweise werden bei der Darstellung der Lichtuhr nur die ganzen Durchläufe gezählt. Man kann die Lichtuhr aber auch, wie hier dargestellt, als „analoge“ Uhr ansehen, bei der auch die Zwischenpositionen des Lichtpulses berücksichtigt werden.
Untersucht wird nun, wie schnell der Lichtpuls die Lichtuhr durchläuft. Zum einen, wenn die Lichtuhr ruht. Zum anderen, wenn sich die Lichtuhr mit einer Geschwindigkeit v nach rechts bewegt.
Sei Alice die Beobachterin im ruhenden und Bob der Beobachter im bewegten Bezugssystem. Betrachten wir zuerst nur die beiden senkrechten Lichtuhren, d.h. die blaue und die grüne Lichtuhr.
Um zu verdeutlichen, dass die Lichtpulse der einzelnen Uhren bei jedem Bild auch die gleiche Strecke zurück gelegt haben, habe ich die Uhren so angeordnet, dass die Lichtpulse immer auf der gleichen, kreisförmigen „Wellenfront“ laufen. Achtung: Diese „Wellenfront“ wird teilweise an den Spiegeln reflektiert. Kleiner Nachteil dieser Darstellung: Die blaue und grüne Uhr sind gegeneinander etwas versetzt.
Betrachten wir zuerst nur die senkrechten Lichtuhren. Bei der ruhenden, blauen Uhr läuft der Lichtpuls mit der Lichtgeschwindigkeit c zwischen den Spiegeln hin und her. Diese Uhr spiegelt Alices „Eigenzeit“ wider. Bei der bewegten, grünen Uhr muss der Lichtpuls die seitwärts Bewegung mit der Geschwindigkeit v mit machen. Deshalb läuft er in Richtung der Spiegel, also senkrecht zur Bewegungsrichtung, nur mit der Geschwindigkeit
Aus Alices Sicht vergeht also Bobs „Eigenzeit“ langsamer. Betrachten wir nun die beiden bewegten Uhren in Bobs System. Die senkrechte, grüne und die waagrechte, rote Uhr, bei der der Lichtpuls parallel zur Bewegungsrichtung der Uhr läuft. Diese beiden bewegten Uhren müssen natürlich, sowohl aus Bobs als auch aus Alices Sicht, gleich schnell gehen. Solange man nur die ganzen Durchläufe zählt, tun sie das auch. Allerdings nur, wenn die senkrechte Uhr um den Faktor Ɣ (gamma) kürzer ist. Die relativistische Längenkontraktion ist also eine notwendige Voraussetzung dafür, dass bewegte Uhren, unabhängig von ihrer Lage, gleich schnell gehen.
Das heißt andererseits aber auch, dass der Lichtpuls bei der waagrechten Uhr, relativ zur Bewegung v, im Mittel nur mit der Geschwindigkeit c/Ɣ2 hin- und her läuft. Aus Alices Sicht läuft, relativ zu Bob, der Lichtpuls in der senkrechten Uhr also mit c/Ɣ, in der waagrechten Uhr aber nur mit c/Ɣ2 hin- und her. Das wird bei der Allgemeinen Relativitätstheorie eine entscheidende Rolle spielen.
Es ist aber noch etwas anderes zu sehen. Alice würde zu Bob sagen: „Hey Bob, deine rote Uhr eiert ja! Zuerst geht sie zu langsam und in der zweiten Hälfte geht sie wieder schneller. Was ist denn da los?“ Bob kann aber kein Eiern bei seiner roten Uhr feststellen. Der Grund dafür ist die „Gleichzeitigkeit“. Ereignisse, die aus Alices Sicht am vorderen und hinteren roten Spiegel gleichzeitig passieren, passieren aus Bobs Sicht zu unterschiedlichen Zeiten, und umgekehrt. Nur aufgrund der unterschiedlichen Gleichzeitigkeit ist alles relativ und die Rollen von Alice und Bob könnten genauso gut vertauscht sein.
Gut, das ging jetzt etwas schnell. Mehr dazu in meinem Podcast zur speziellen Relativitätstheorie.
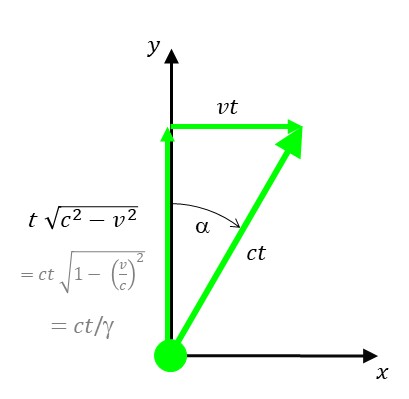
Bei der grünen, seitwärts propagierenden Lichtuhr hat der Lichtpuls in x-Richtung eine Geschwindigkeitskomponente v. Dadurch hat er in y-Richtung eine dem Satz von Pytagoras entsprechende, kleinere Geschwindigkeit c/Ɣ. Der Term 1/√(1-v2/c2) wird in der Relativitätstheorie gamma (Ɣ) -Faktor genannt.
In diesem Fall hat v gerade die Hälfte der Lichtgeschwindigkeit c.
Für den Winkel alpha gilt:
sin(alpha)=v/c
tan(alpha)= Ɣ * v/c